A fast method to round a double to a 32-bit int explained note

Quote:

Between 2^52=4,503,599,627,370,496 and ^253=9,007,199,254,740,992 the representable numbers are exactly the integers
This follows from the fact that the mantissa is 52 bits wide.

The other interesting fact about adding 2^51+2^52 is that it affects the mantissa only in the two highest bits - which are discarded anyway, since we are taking only its lowest 32 bits.












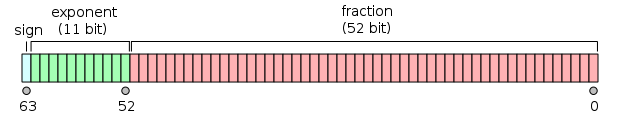
So we add 2^51+2^52 and get the lowest 32 bits via a cast than we can get the integer from double.

#define double2int(i, d) \
    {double t = ((d) + 6755399441055744.0); i = *((int *)(&t));}

Ref:
      1. A fast method to round a double to a 32-bit int explained
      2. Double-precision floating-point format